Real Numbers: It is the combination of “rational” and “irrational” numbers.
Rational Numbers: Those numbers which can be expressed in the form of p/q, where ‘p’ and ‘q’ are integers and ‘q’ is not equal to zero are called rational numbers. example: 0, 2, 4/7, 1.2, 1.2/3 etc.
OR
Rational numbers are those numbers whose decimal expansion is either terminating or repeating/recurring non-terminating. example:[repeating non-terminating decimal expansion] 0.333333….., 2.1666666….., [terminating decimal expansion] 1.75, 5.625 etc.
Irrational Numbers: Those numbers whose decimal expansion is neither terminating nor repeating are called irrational numbers. example: √2, √3, π(pi), 1.100100010000………….. etc.
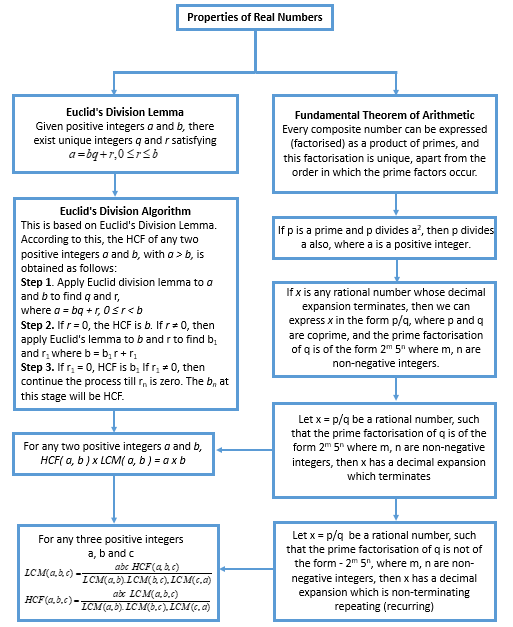
Euclid’s Division Lemma
Euclid’s division lemma states that for any two positive integers, say ‘a’ and ‘b’, the condition ‘a = bq +r’, where 0≤ r< b always holds true. Mathematically, we can express this as ‘Dividend = (Divisor × Quotient) + Remainder’. A lemma is a statement that is already proved. Euclid, a Greek mathematician, devised Euclid’s division lemma for finding the HCF of numbers.
Euclid’s Division Lemma (lemma is similar to a theorem) says that, for given two positive integers , ‘a’ and ‘b’, there exist unique integers, ‘q’ and ‘r’, such that: a = bq+r , where 0≤r<b.
The integer ‘q’ is the quotient and the integer ‘r’ is the remainder. The quotient and the remainder are unique. In simple words, Euclid’s division lemma statement is that if we divide an integer by another non-zero integer, we will get a unique integer as quotient and a unique integer as remainder.
We can write the above scenario mathematically as: ‘Dividend = (Divisor × Quotient) + Remainder’. The above scenario shows the way of representing the division of positive integers with the help of Euclid’s division lemma.
How to Find HCF By Euclid’s Division Lemma?
Euclid’s division lemma has many uses or applications. Let’s learn about two of the most important uses of this algorithm. We use Euclid’s division lemma to find the HCF of large numbers which is typically difficult to calculate using basic HCF calculation techniques. The HCF of two numbers can be calculated with the help of Euclid’s division lemma by following these steps.
Let’s take two numbers ‘c’ and ‘d’ for which we need to find the HCF such that c > d.
Step 1:- Apply Euclid’s division lemma to ‘c’ and ‘d’. We can find whole numbers, ‘q’ and ‘r’ such that c = dq + r, 0 ≤ r < d.
Step 2:- If r = 0, ‘d’ is the HCF of ‘c’ and ‘d’. If r ≠ 0, apply the division lemma again to ‘d’ and ‘r’.
Step 3:- Continue the process till the remainder is zero. The divisor at this stage will be the required HCF.
Example: Find the HCF of 320 and 132.
solution: Since 320>132 , we use EDL to 132 and 320;

here in the last step r=0 ,therefore HCF(132,320)=4
EXERCISE 1.1


Q.3
An army contingent of 616 members is to march behind an army band of 32 members in a parade. The two groups are to march in the same number of columns. What is the maximum number of columns in which they can march?
Solutions:
No. of army contingent members=616
No. of band members=32
Maximum number of columns = HCF of (616, 32)
For finding the HCF we should apply Euclid’s division algorithm

Therefore HCF of 616,32=8
hence maximum no. of columns in which they can march=8
Q.4 Use Euclid’s division lemma to show that the square of any positive integer is either of the form 3m or 3m + 1 for some integer m.
Solution: Let ‘a’ be any positive integer and ‘b’ =3
then by using EDL ,we get a=bq+ r; 0 ≤ r < 3 for some integer ‘q’
So, the possible values of ‘a’ are 3q or 3q + 1 or 3q + 2
when a=3q
squaring both sides ,we get
a2 = 9q2 =3(3q2) =3m
where, m = 3q2
Case II: when a=3q+1
squaring both sides ,we get
a2 = (3q+1)2
3(3q2 + 2q) + 1=3m+1
where, m = (3q2 + 2q)
Case III: when a=3q+2
squaring both sides we get,
a2 = (3q+2)2 =9q2 + 12q+4
=3(3q2 + 4q +1) + 1 =3m+1
where, m = (3q2 + 4q +1)
Thus, we see that a2 is of the form 3m or 3m + 1 where, m is any positive integer.
Hence, it can be said that the square of any positive integer is either of form 3m or 3m + 1
Q.5 Use Euclid’s division lemma to show that the cube of any positive integer is of the form 9m,9m+1 or 9m+8
Answer: let ‘a’ be any positive integer and ‘b’=3
According to Euclid’s Division Lemma
a = 3q + r ;(0 ≤ r < 3)
So possible remainders are: 0, 1 or 2.
Case 1: When r = 0, the equation becomes
a = 3q
Cubing both the sides
a3 = (3q)3
a3 = 27 q3
a3 = 9 (3q3)
a3 = 9m
where m = 3q3
Case 2: When r = 1, the equation becomes
a = 3q + 1
Cubing both the sides
a3 = (3q + 1)3
a3 = (3q)3 + 13 + (3 × 3q × 1)(3q + 1)
a3 = 27q3 + 1 + 9q × (3q + 1)
a3 = 27q3 + 1 + 27q2 + 9q
a3 = 27q3 + 27q2 + 9q + 1
a3 = 9 ( 3q3 + 3q2 + q) + 1
a3 = 9m + 1
Where m = ( 3q3 + 3q2 + q) is some integer
Case 3: When r = 2, the equation becomes
a = 3q + 2
Cubing both the sides
a3 = (3q + 2)3
a3 = (3q)3 + 23 + (3 × 3q × 2) (3q + 2)
a3 = 27q3 + 8 + 54q2 + 36q
a3 = 27q3 + 54q2 + 36q + 8
a3 = 9 (3q3 + 6q2 + 4q) + 8
a3 = 9m + 8
Where m = (3q3 + 6q2 + 4q)
therefore ‘a’ can be any of the form 9m or 9m + 1 or, 9m + 8.